
Looking at the same object from two different positions can determine its distance.
Our Milky Way galaxy contains many exotic and newly discovered objects, including black holes, microquasars and supernova remnants. Nevertheless the best and usually only reliable way to determine the distances to these objects has been known for thousands of years and is the standard technique used to measure distances here on Earth for construction and determining property boundaries.
The same technique is used by many animals to build a three dimensional view of their surroundings.
The basic idea is always the same: measure the shift in the apparent direction of an object from two different positions. This shift (measured as an angle) is called a parallax.
Professional surveyors (whether property surveyors or galactic surveyors) can then use basic trigonometry to compute the distance to the object if they have the distance between the two measurements and the parallax.
Animals with two forward facing eyes such as apes and owls can use a similar technique to build a three-dimensional model of their immediate environment. At least some scientists have concluded that the head-bobbing seen in pigeons and many other bird species with eyes on opposite sides of the head also serves to provide parallax data from two different positions. (eg. see this PDF abstract).
Astronomical parallax
In astronomy the distances involved are much larger than for ordinary surveying projects and so a larger baseline between the two measurement positions is required. Fortunately, the Earth's orbit around the Sun conveniently provides a sufficient distance. The radius of the Earth's orbit (called the astronomical unit) is well known. In fact it is so well known that it is used to define the parsec, the basic unit of distance beyond our solar system. A parsec is the distance of an object with a parallax of one arc-second (that is a 60th of a 60th of a degree) when using the radius of the Earth's orbit as a baseline. The nearest star has a distance of 1.3 parsecs and the centre of the galaxy has a distance of about 8000 parsecs.
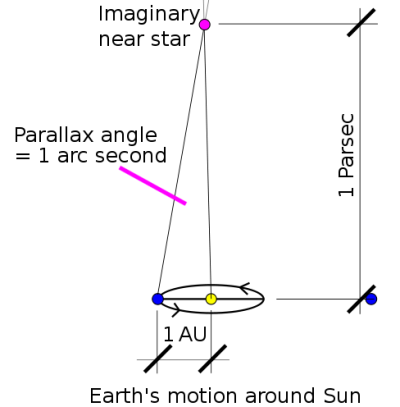
Measuring the distance of objects in parsecs is in principle easy. In practice it is not so simple.
In principle, measuring astronomical parallax is easy: measure the position of an object in the sky relative to other objects known to be much further away (eg. quasars in distant galaxies). Wait six months for the Earth to orbit to the opposite side of the sun. Measure the position again. Use the radius of the orbit and the change in position to determine the distance to the object. It turns out that using the Earth's orbit as a baseline is enough to determine the distance of any object in the Milky Way - even objects on the far side of the galaxy.
Of course it is not so easy. The main difficulty is measuring the parallax accurately. Stars and other Milky Way objects are so distant that the first accurate parallax measurement for a star (61 Cygni) was made by Friedrich Bessel only in 1838 even though the technique was obvious once it was accepted that the Earth orbits the Sun. The first large scale parallax measurements were only carried out by the Hipparcos satellite, launched in 1989. Even then, Hipparcos was only able to reliably measure parallax for a few thousand stars located at a distance of at most 2-300 parsecs. This is not even as far as the Orion nebula within the local stellar neighbourhood.
Technology has advanced quickly since Hipparcos and the Gaia satellite, scheduled to be launched in 2012, is expected to measure parallax for about 1 billion stars scattered over a distance of several thousand parsecs. Gaia will provide a major step forward in mapping our Milky Way in great detail.
But Gaia will not finish the job. Gaia will measure parallax for optically visible stars, and much of the Milky Way, especially the most interesting parts in the central bar and spiral arms, is obscured by dust. Another technology is required. Fortunately, that technology is now available.
Radio to the rescue
Hubble is by far the most famous telescope. But it is not the most powerful telescope available. The most powerful telescopes are the much less known EVN (based in Europe) and VLBA (based in the United States). These networks of radio telescopes use sophisticated computer and communication technology called very long baseline interferometry (VLBI) to function as single continent spanning telescopes - the greatest eyes-on-the-sky ever created.
Like Gaia, the VLBI networks (which also include several smaller networks based in Canada, Australia, Japan and elsewhere) can measure parallax accurately enough to determine the positions of objects across the galaxy. Unlike Gaia, these networks can pierce the Milky Way's clouds of dust to determine the distances to masers - focused sources of microwave radiation associated with star formation regions. By mapping the masers, the VLBI networks can determine the exact locations of the Milky Way's star formation regions and so map the galaxy as a whole.
So far the VLBI networks have determined the positions of about a dozen or so carefully selected objects. This has already been enough to start to determine the positions of key parts of the Milky Way's spiral arms. Plans have been announced to dramatically expand the number of accurate radio parallax measurements in the near future. Galaxy Map will continue to keep track of these important developments.
Substitutes for parallax
Reliable VLBI parallax measurements have only started to become available within the past decade. Before this, astronomers were forced to use much less reliable techniques to estimate the distances of objects more than a few hundred parsecs from our solar system. The two main techniques were kinematic and photometric distance estimates.
Kinematic distance estimates
When an object moves towards an observer, its light is shifted to higher (blue) frequencies. When the object moves away, its light is shifted to lower (red) frequencies. This fact was first reported by the Austrian physicist and astronomer Christian Doppler in 1842. Astronomers immediately began to use this fact to measure the movement (kinematics) of stars and star clusters. These velocity measurements led the Dutch astronomer Jan Oort in 1928 to propose that the Milky Way rotates. At about the same time, other astronomers, including Edwin Hubble, concluded that the very high red shifts of distant galaxies meant that the universe was expanding.
If astronomers made the assumption that velocities observed for Milky Way stars or nebulae were due primarily to the rotation of the Milky Way and that the Milky Way had a simple rotation model, then they could use this model to determine two possible distances for each star or nebula. Astronomers then used several techniques to choose between these two possible estimates. Even better, blue or red shifts could be measured for the large clouds of hydrogen gas detected across the Milky Way by radio telescopes. For much of the second half of the twentieth century (and especially in the 1950s and 1960s) it was believed that kinematic distance estimates could map the Milky Way.
A very clear description of the process used to make kinematic distance estimates (including the formulas used) can be found in this recent paper.
It is now known from other distance estimates (especially those now available from VLBI parallax) that the main assumptions behind many kinematic distance estimates were incorrect. The Milky Way does not have a simple rotation curve (different kinds of objects rotate at different rates). The velocities measured within much of the Milky Way are strongly affected by local gas movements such as expanding bubbles and streaming within spiral arms and not just the rotation of the galaxy as a whole.
Of course astronomers have always known that the assumptions behind kinematic distance estimates were not always true. But now it is known that many kinematic estimates grossly distort the distance to important parts of the Milky Way. For example, VLBI parallax suggests that the Perseus arm in the second galactic quadrant lies at a distance of about 2500 parsecs rather than 5000 parsecs, and the Sagittarius arc is also much closer (about 1000-1500 parsecs instead of 2000-3000 parsecs).
Perhaps the best that can be said is that objects with a similar velocity and direction are more likely to lie at the same distance than those with different velocities. So velocity measurements help to group objects together but do not determine the distances for those groups. You can read more about kinematic distance estimates and view images illustrating two of the major velocity data sets available in the chapter on Velocity.
Photometric distance estimates
Stellar spectra reveal an amazing amount of information about a star. Not only does a red or blue shift reveal its velocity but the details of the spectrum often reveal its chemical composition, its temperature and sometimes even its approximate size. If the size and temperature are known, then it is possible to calculate the luminosity. Comparing the actual and apparent luminosity of a star should in theory make it possible to calculate its distance.
As with kinematic distance estimates, there are a number of problems with this photometric approach. Estimating distance from luminosity requires a model for the distribution of dust in the Milky Way and this distribution (especially in the spiral arms) is not simple. Determining the size of a star is not trivial, although this problem can be partially overcome by using probabilistic calculations applied to entire star clusters rather than individual stars. Finally, most photometric techniques apply only to optically visible stars and star clusters. Recent infrared observations have shown that many and probably most star forming regions are obscured by thick clouds of dust.
On the whole, recent VLBI parallax measurements have shown that photometric distance estimates, when available, tend to be considerably more accurate than kinematic estimates. Nevertheless, now that accurate parallax measurements are or will soon be available for many Milky Way objects, they should be preferred over any less reliable method.
