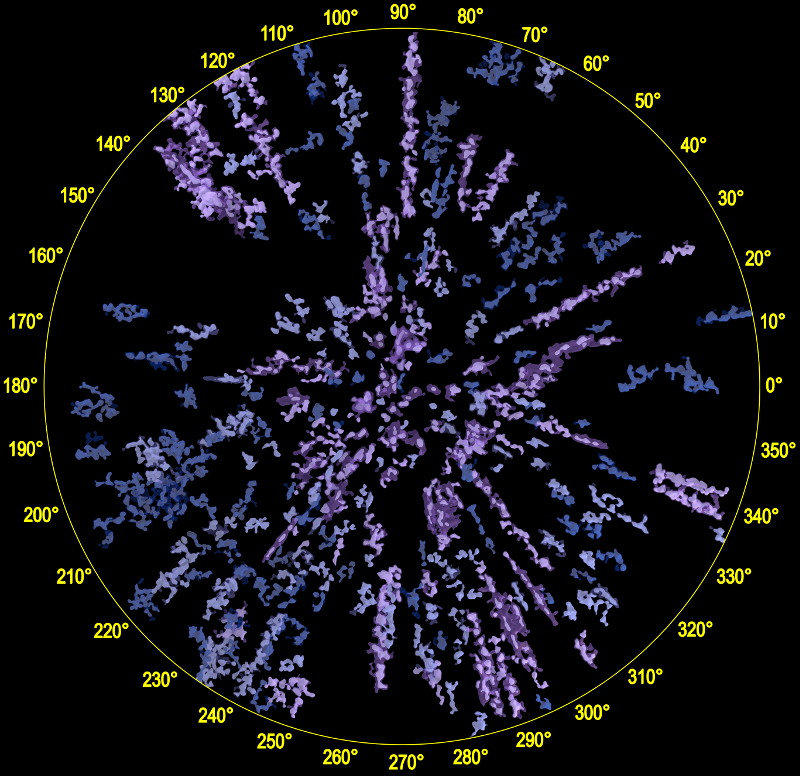
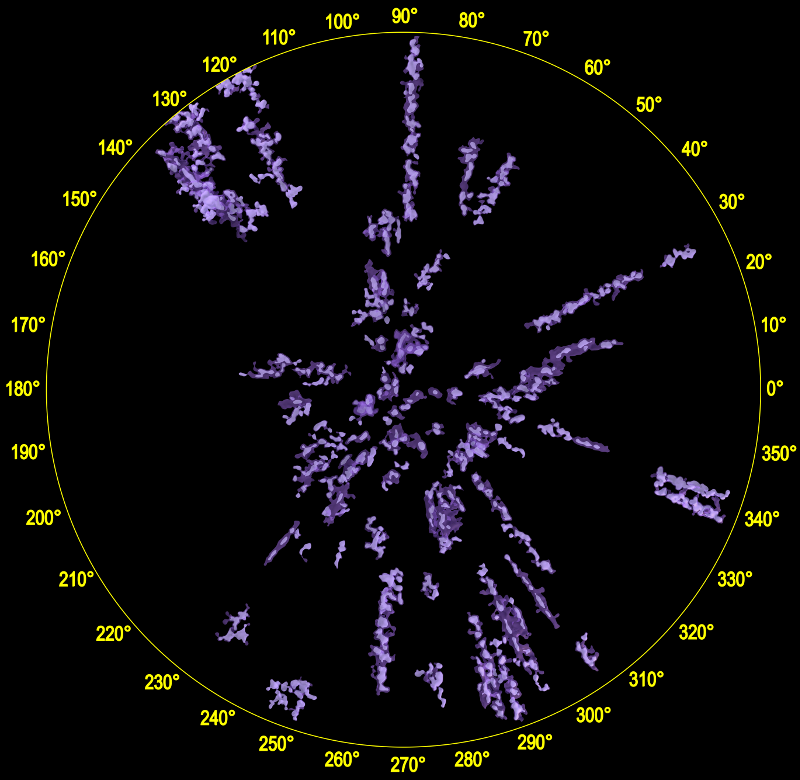
Gaia mapping resources and data sources
Below is a list of map resources, a brief description of how they were derived, and a bibliography of data sources.
Latest full zoomable map
This zoomable map goes out to a radius of 6000 parsecs (about 20 thousand light years)
http://gruze.org/galaxymap/map_2020/
Here is a zip with the background image and an SVG file with all the labels:
http://gruze.org/galaxymap/map_2020/svg_release.zip
Map out to 800 parsecs with star density clumps and optional luminous star overlay
Includes zoomable online maps, pdfs and SVG source.
Described here:
http://galaxymap.org/resources/
Meshes
Here is a zip with all the meshes used to create the maps:
http://gruze.org/galaxymap/meshes/meshes.zip
Blender file
Here is a zip with the above meshes, plus appropriate camera, lighting and materials in a .blend file:
http://gruze.org/galaxymap/map_2020/galaxy_map_2020.zip
Object data
Here is a csv file with raw data for 157 masers, 2082 open clusters, 232 HII regions and 86 OB associations that appear on the maps:
http://gruze.org/galaxymap/map_2020/map_object_list.csv
License
All materials released under the Creative Commons By Attribution 4.0 license.
Credit: Kevin Jardine (Twitter: @galaxy_map)
Overview
How do you map 1.7 billion stars?
Here's a recent presentation that tries to answer this question. More detailed references can be found below:
The revolutionary Gaia DR2 release on 25 April 2018 contained an amazing amount of information that is a challenge to visualize.
Simply displaying the stars would be worse than an image of a Sahara sandstorm. Fortunately, there is another alternative.
The game plan
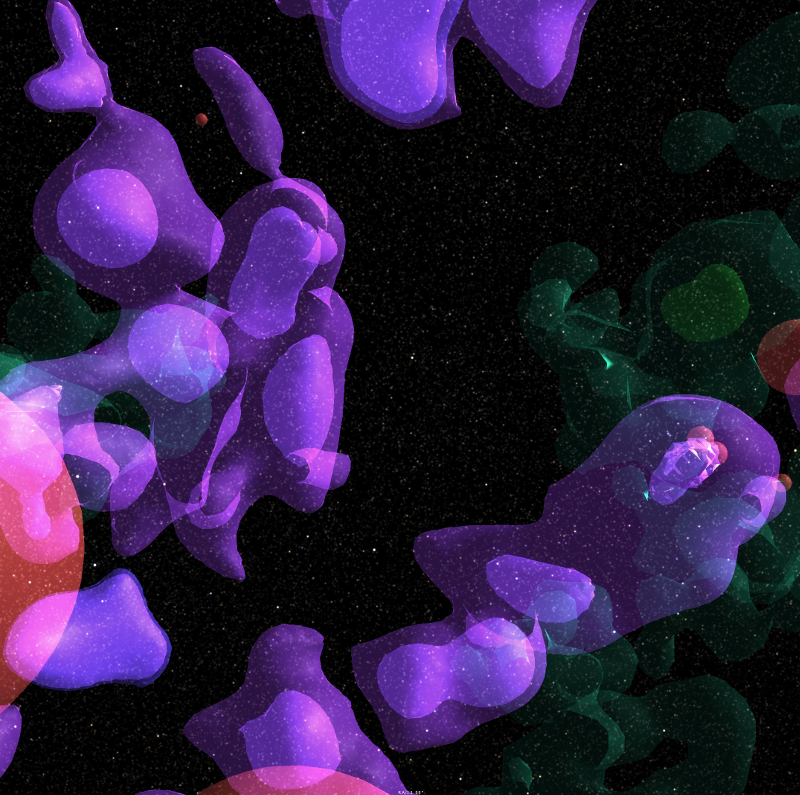
A technique called density isosurfaces is more commonly used to generate images from medical MRI scans.
In this technique we generate 3D surfaces consisting of a common density value, much like we can use contour lines on topographic maps to show regions of common elevation. In MRI scans this is human tissue density. For galaxy mapping we can use star density, counting the number of stars per cubic parsec. We can, in a way, use Gaia data to do an MRI scan of the Milky Way.
There is a crucial point about stars that affects mapping using this density technique.
This is that older cooler stars cannot be seen from a great distance, and tend to move around randomly from their place of birth. A random starscape does not give anything interesting to map.
So if you are going to make a large map, it often works better to focus on younger, hotter stars. These are usually closer to their birth places and can be seen for a long distance. And if you are going to make a smaller map, you can include cooler stars as well, but best to focus on large dense clumps as these will be closer to their birth places than a less dense random haze.
There is one major barrier to implementing this plan for larger maps, and that is dust. Dust can obscure and redden young hot stars and make them appear to be older cooler stars instead.
There was an attempt to provide information about reddening in the Gaia DR2 release, but it is not accurate enough for mapping. This is likely to be improved in future Gaia releases.
For this reason, astronomers have prepared special dereddened hot star subsets of the Gaia data set by adding additional information from other surveys. It turns out that infrared data is especially valuable in determining a star's true nature because infrared radiation is less affected by dust.
The hot star data sources
The Galaxy Map hot star density maps are derived from three star databases. The first is a set of about 600 thousand Gaia stars that have been dereddened using the 2MASS infrared survey. This data set is described in this paper:
Poggio, E., R. Drimmel, M. G. Lattanzi, R. L. Smart, A. Spagna, R. Andrae, C. A. L. Bailer-Jones et al. "The Galactic warp revealed by Gaia DR2 kinematics" Monthly Notices of the Royal Astronomical Society: Letters 481, no. 1 (2018): L21-L25.
(Thank you to Eloisa Poggio for providing the latest version of this data set on 30 August 2019.)
This was merged with a second StarHorse data set with an additional 200 thousand hot stars with (BPRP0 < -0.1) and (SH_GAIAFLAG == '000') and (SH_OUTFLAG == '00000') from:
Anders, Friedrich, et al. "Photo-astrometric distances, extinctions, and astrophysical parameters for Gaia DR2 stars brighter than G= 18." Astronomy & Astrophysics 628 (2019): A94.
Both these hot star data sets are missing stars close to the Sun. So they are supplemented with a database of about 10 thousand OB stars within 1 kpc using SIMBAD colours and Bailer-Jones distances derived from Gaia DR2.
Other star data sources
Star clumps with no temperature or colour limits are computed using Bailer-Jones distances for older maps. Recent maps use a zero point correction of -0.029 and the formula: distance in parallax = 1000/(plx-zero_point_correction) .
OB associations
OB association positions were computed from the median distance to the member stars given in the data set first described in:
Humphreys, R. M. "Studies of luminous stars in nearby galaxies. I. Supergiants and O stars in the Milky Way" Astrophysical Journal, Suppl. Ser., Vol. 38, p. 309 - 350.
HII regions
HII region positions were computed from the distance to known ionizing open clusters or using the median distance to known ionizing stars.
Star clusters
The newest maps use the Gaia DR2 open cluster catalog described in:
Cantat-Gaudin, T., et al. "Painting a portrait of the Galactic disc with its stellar clusters." arXiv preprint arXiv:2004.07274 (2020).
We calculate the cluster distances using the cluster parallax and a zero point correction of -0.029. distance in parallax = 1000/(plx-zero_point_correction)
We use this calculation rather than the distances provided in the 2020 open cluster catalog because it ensures that the clusters align with the Gaia density clumps.
For older maps:
The main data set for the star clusters was kindly provided by Tristan Cantat-Gaudin on 10 December 2019 and is described in this paper:
Cantat-Gaudin, T., and F. Anders. "Clusters and mirages: cataloguing stellar aggregates in the Milky Way." Astronomy & Astrophysics 633 (2020): A99.
This was supplemented by the new cluster data set described in:
Liu, Lei, and Xiaoying Pang. "A catalog of newly identified star clusters in GAIA DR2." The Astrophysical Journal Supplement Series 245.2 (2019): 32.
I removed some Liu Pang clusters that clearly duplicated Cantat-Gaudin clusters.
And also supplemented by the new clusters contained in this paper:
Castro-Ginard, A., et al. "Hunting for open clusters in Gaia DR2: 582 new open clusters in the Galactic disc." Astronomy & Astrophysics 635 (2020): A45.
Dust
Rosine Lallement has led a team that has published several important papers on dust distribution derived from the Gaia data. The most recent dust data set is used on our maps and is described in:
Lallement, R., et al. "Gaia-2MASS 3D maps of Galactic interstellar dust within 3 kpc." Astronomy & Astrophysics 625 (2019): A135.
Molecular Clouds
Many of the dust cloud labels are derived from the molecular cloud maps contained in:
Zucker, Catherine, et al. "A compendium of distances to molecular clouds in the Star Formation Handbook." Astronomy & Astrophysics 633 (2020): A51.
Luminous stars
Several of the maps contain overlays of luminous stars. These are determined by taking Gaia DR2 stars with low astrometry errors (err/plx< 0.2, G > 5 and RUWE < 1.4). If these stars are in the 2MASS and StarHorse catalogs and the StarHorse quality flags are (SH_GAIAFLAG == '000') and (SH_OUTFLAG == '00000') and the 2MASS quality flag is 'AAA', then we use the StarHorse dereddened absolute magnitude, otherwise we calculate the absolute magnitude using Gaia G and the parallax with a zero point correction of -0.029. We've also supplemented this data set with Hipparcos 2007 re-analysis stars with err/plx < 0.2 if they are not in our list.
We filter out Gaia stars with G < 5 because Gaia stars with very high relative magnitude are known to have unreliable parallaxes, as described in this research note:
https://iopscience.iop.org/article/10.3847/2515-5172/ab2632
You can download a list of about 38 thousand luminous stars with absolute magnitude < -2 and distances within 3 kpc here:
http://gruze.org/galaxymap/luminous/all_3kpc_luminous_merged.zip
Tools
MeshLab, Blender and Inkscape, plus many (many) Python scripts.
Acknowledgements
Star density mapping was pioneered for the Hipparcos data set and inspired the Galaxy Map initiatives. These results are described in the paper:
Bouy, H., and J. Alves. "Cosmography of OB stars in the solar neighbourhood." Astronomy & Astrophysics 584 (2015): A26.
Some recent maps of the solar neighbourhood appear in:
Zari, E., et al. "3D mapping of young stars in the solar neighbourhood with Gaia DR2." Astronomy & Astrophysics 620 (2018): A172.
This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium).
Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Many members of the Gaia team have provided useful advice and aid but in particular I would like to thank Anthony Brown for strongly encouraging this project and Ronald Drimmel for providing invaluable data and technical advice. I would also like to thank Stefan Payne-Wardenaar for help with Blender materials.